Нужно найти пределы но Только НЕ методом Лапиталя. С решением.

Ответы

LymarIvan 06.08.2021 21:22

Объяснение:

$\lim_{x \to -2} \frac{2x^{3} + 16}{19x^{3} + 57x^{2} + 19x -38} = \lim_{x \to -2} \frac{2(x^{3} + 8)}{(x + 2)(19x^{2} + 19x - 19)} = \lim_{x \to -2} \frac{2(x + 2)(x^{2} -2x +4)}{19(x + 2)(x^{2} - x -1)} = \lim_{x \to -2} \frac{2(x^{2} -2x +4)}{19(x^{2} - x -1)} = \frac{2((-2)^{2} - 2 * (-2) + 4)}{19((-2)^{2} - 2 -1)} = \frac{2(4 + 4 + 4)}{19(4 - 2 -1)} = \frac{24}{19}$

Разложим на множители: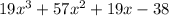 $19x^{3} + 57x^{2} + 19x -38$

$19x^{3} + 57x^{2} + 19x -38 = 0$

Проверим корень -2:

$19 * (-2)^{3} + 57 * (-2)^{2} + 19 * (-2) - 38 = -152 + 228 - 38 - 38 = 228 - 228 = 0$

Следовательно x = -2, корень уравнения.

По следствию из теоремы Безу разделим многочлены столбиком:

$(x + 2)(19x^{2} + 19x - 19) = 19(x + 2)(x^{2} - x -1) = 19x^{3} + 57x^{2} + 19x -38$

2) $\lim_{x \to 1} \frac{\sqrt{x + 8} - 3}{\sqrt{5 - x} - 2 } = \lim_{x \to 1} \frac{(\sqrt{x + 8} - 3)(\sqrt{x + 8} + 3)(\sqrt{5 - x} + 2)}{(\sqrt{5 - x} - 2)(\sqrt{5 - x} + 2)(\sqrt{x + 8} + 3) } = \lim_{x \to 1} \frac{(x + 8 - 9)(\sqrt{5 - x} + 2)}{(5 - x -4 )(\sqrt{x + 8} + 3)} = \lim_{x \to 1} \frac{(x - 1)(\sqrt{5 - x} + 2)}{(1 - x)(\sqrt{x + 8} + 3)} = \lim_{x \to 1} \frac{(x - 1)(\sqrt{5 - x} + 2)}{-(x - 1)(\sqrt{x + 8} + 3)} = - \lim_{x \to 1} \frac{\sqrt{5 - x} + 2}{\sqrt{x + 8} + 3 }$ $= - \frac{\sqrt{5 - 1} + 2}{\sqrt{1 + 8} + 3} = -\frac{2 + 2}{3 + 3} = -\frac{4}{6} =-\frac{2}{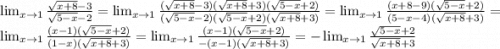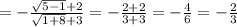3}$