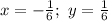Нужно найти х и у из тождества, но у меня получается уравнение с тремя неизвестными
Другие вопросы по теме Алгебра
Популярные вопросы
- Отдает или принимает электроны ne? ...
1 - Скажите , как человек использует реку инд, какие пользы инд приносит людям?...
1 - Найдите следующие отношения и напишите что показывает каждое из отношений...
1 - Написать 2-3 предложения каждого стиля речи 30 !...
3 - Дайте аргументированный ответ на проблемный вопрос во что верит автор комедии недоросль...
3 - Complete the sentences with the words in the box: , буду признателен.так-то учил...
1 - Два прямоугольника имеют одинаковый периметр длина первого прямоугольника 9 см...
3 - Как проверить слова пар_ходы пут_шествий см_стерили пар_возы д_роги х_роший р_ботник...
1 - 5. выпишите предложение с прямой речью. (знаки препинания не расставлены) расставьте...
2 - 4complete the conversation with the useful language. useful language offers requests...
2
Смысл задачи: найти такие x и y, чтобы это равенство было справедливо при всех допустимых значений a (то есть для всех, кроме -4 и 2).
1-й
2-й
Запишем равенство в виде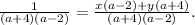
знаменатели в левой и правой части совпадают, поэтому совпадают числители:
x(a-2)+y(a+4)=1.
Дальше у нас есть две возможности рассуждения. При первой подставляем в это равенство a=2, находя при этом y=1/6, а затем подставляем a=-4, находя x=-1/6.
При втором рассуждения запишем равенство в виде
(x+y)a+(-2x+4y)=1. Поскольку это равенство должно быть справедливо при всех значениях a, получаем систему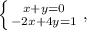 решив которую, получим те же значения x и y.
решив которую, получим те же значения x и y.
ответ: