Нужно. напишите доказательство того, что а= 10^24+120 делится на 11

Признак делимости на 11:

разность суммы цифр, стоящих на нечетных позициях (при нечетных степенях разложения числа), и суммы цифр, стоящих на четных позициях (при четных степенях разложения числа), должна делиться на 11.

Число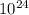 - это 1 и следом за ней 24 нуля.

Если к числу прибавить 120, получится 100...00120

То есть, на нечетных позициях стоит 1, много нулей, ещё 1, и последний 0.

А на нечетных позициях стоит много нулей и 2.

Первая сумма 1+1=2

Вторая сумма 2.

Их разность равна 2-2=0, 0 делится на 11, значит, и само исходное число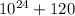 делится на 11.

P.S. про разложение - имел в виду это:

Объяснение:

Заметим:

10¹ = 10             (двузначное число)

10² = 100          (трехзначное число)

10³ = 1 000       (четырехзначное число)

10⁴ = 10 000     (пятизначное число)

.............................................................

Мы можем заметить, что если степень четная, то  число будет иметь нечетное число цифр...

По условию - степень четная, значит в записи числа 10²⁴ нечетное число знаков.

А теперь рассмотрим заданное число а.

a = 100...00120 ( здесь первая 1 стоит на нечетном месте)

Сумма цифр, стоящих на нечетных местах равна (1+0+... 1+0) = 2

Сумма цифр, стоящих на четных местах равна (0+0+...+2) = 2

Эти суммы РАВНЫ, значит заданное число делится на 11.

Вспомним признак делимости на 11: