Нужна с алгеброй Решите уравнение:
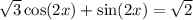
Другие вопросы по теме Алгебра
Популярные вопросы
- Делителем натурального числа а называют натуральное число,на которое а...
1 - Какая роль в сохранении культурного достояния страны отводится государству?...
1 - Составьте предложения с причастными оборотами, используя данные ниже слова....
1 - Какой звук обазначает буква н глухой или звонкий...
1 - Бежит лиса по снегу,хвостом следы заметает. какое это предложение простое...
3 - Составьте сложное предложение со словами: углубит, . заранее !...
3 - Написать план жизнь египетского вельможи опираясь на параграф 8...
1 - Дроби к наименьшему общему знаменателю7/60, 13/540 и 9/20; 52/105, 7/95...
1 - Выпиши из первого абзаца дополнения со словами к которым они относятся...
3 - Найти словосочетания в предложении- отечеством мы зовем нашу страну потому,...
1
вот, ответ..)). ......
Вод держи надеюсь правильно
левой части воспользуемся формулой со вс аргументом: корень из (3+1)=2
2sin(2x+pi/3)=sqrt 3 sin(2x+pi/3)=sqrt 3)/2
2x+pi/3=(-1)^n pi/3+pi n 2x= (-1)^n pi/3-pi/3+pi n
x=(-1)^n pi/6-pi/6+pi n/2
b) sin 2x=2tgx/(1+tg^2x)
уравнение примет вид: 2tgx/(1+tg^2x) +1/tgx-3=0
2tg^2x+2+2tg^2x-3tgx-3tg^3x=0 tgx не=0
y=tgx 3y^3-4y^2+3y+2=0
y=1 -корень уравнения . Разделив левую часть уравнения на (у-1), получим:
(У-1)(3y^2-y+2)=0 Имеет только один действ. корень у=1 Тогда tgx=1
x = pi/4+pi n