1. Алгебра
  2. Номер 8, главное правильно

Номер 8, главное правильно


Номер 8, главное правильно

диана2458 диана2458    1   23.02.2022 14:24    0

Ответы
ehadid ehadid  23.02.2022 14:30

Доказать, что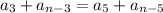   a_3+a_{n-3}=a_5+a_{n-5}  .

Применим формулу общего члена арифметической прогрессии .

\boxed{\ a_{k}=a_1+d\, (k-1)\ }a_3=a_1+2d\ \ ,\ \ \ a_{n-3}=a_1+d\, (n-4)=a_1+dn-4dunderline{a_3+a_{n-3}}=a_1+2d+(a_1+dn-4d)=\underline{2a_1-2d+dn}a_5=a_1+4d\ \ ,\ \ \ a_{n-5}=a_1+d\, (n-6)=a_1+dn-6dunderline{a_5+a_{n-5}}=a_1+4d+(a_1+dn-6d)=\underline{2a_1-2d+dn}

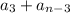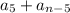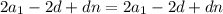Получили , что если сравнить выражения  a_3+a_{n-3}  и выражение  a_5+a_{n-5}  , то они окажутся равными :  2a_{1}-2d+dn=2a_1-2d+dn  .

Значит, равенство доказано .

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
liza1430 liza1430  02.04.2020 14:04
Продифференцировать данные функции...
Androidekstas Androidekstas  02.04.2020 14:00
У выражение 3(0,4x+y)−6(3x−y) и определи его значение, если x=5 и y=3,4....
greatmagister greatmagister  02.04.2020 13:58
Укажи пару чисел, являющуюся решением уравнения 2x-y=16А)-1;16Б)2;0В)1;2Г)0;16Д)0;-16...
Riki008 Riki008  02.04.2020 13:58
Представь квадрат двучлена в виде многочлена:(1/16 z² −9/ 10)².(Переменную вводи с латинской раскладки.) / - черта дроби​...
g2004 g2004  02.04.2020 13:57
Знайдіть найбільше значення функції f(х) = x4- 2 x2 + 3 на відрізку [-1;3]....
aidana70 aidana70  02.04.2020 13:57
Дріт завдовжки 50м розрізали на дві частини так, що одна з них виявилась на 1м коротшою від половини другої. Знайдіть довжину кожної частини.​...
dasha45671dfd dasha45671dfd  02.04.2020 13:57
Складіть зведене квадратне рівняння корені якого є числа 3 і 2...
Sachak95 Sachak95  02.04.2020 13:54
Скільки коренів має рівняння 7x²-x+1=0;D=-27...
Huran Huran  02.04.2020 14:09
Продифференцировать данные функции....
DaNa0414 DaNa0414  02.04.2020 14:08
470. Приведена таблица размеров обуви 50 восьмиклассниц: Измерения:34 35 36 37 38 39 40 Частота: 5 7 10 15 7 4 2Используя данные: 1) постройте таблицу относительных частот;...

Популярные вопросы