Ниже какого значения должен быть параметр а, чтобы при любом значении параметра b уравнение 3х²-12|х|-7|b-3a+6|+3|b-9|-2b+15a=75 имело ровно два корня?
Другие вопросы по теме Алгебра
Популярные вопросы
- Каковы причины поражения французской армии? 1812г. (если можно по пунктам) заранее...
1 - Двое рабочих изготавливали одинаковые детали обслуживали обслуживал один изготавливал...
2 - План к рассказу одиссей на острове циклопов.плофией! заранее !...
2 - При переработке молока получилось 8% творога.сколько творога можно получить из...
3 - Подчеркни слово которое не евляется синонимы к слову дорога...
1 - Калий , йодит , вода , натрий сульфид , калий ёдит , куда они идут - в коволентную...
2 - Величины и явления, используемые в устройствах и эксплуатации автомобиля...
2 - Написать сочинение. мини. 《осень за моим окном》...
2 - Сопоставление характеристики вольги и микулы...
3 - Характеристика героев сказание о борисе и глебе...
1
(см. объяснение)
Объяснение:
Введем функцию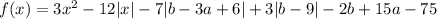 .
.
Заметим, что перед нами уравнение двух парабол, склеивающихся в фиксированной точке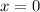 .
.
Этот график может ездить только вверх-вниз в зависимости от значений параметров и
и 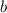 .
.
Уравнение может иметь ровно два корня при любом значении параметра
может иметь ровно два корня при любом значении параметра 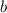 только, если
только, если 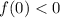 .
.
Тогда перейдем к неравенству:
Построим его в координатах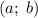 .
.
(см. прикрепленный файл)
Получили, что при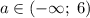 исходное уравнение имеет ровно два различных корня при любом значении параметра
исходное уравнение имеет ровно два различных корня при любом значении параметра 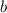 .
.
ответим теперь на вопрос задачи: ниже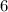 .
.
Задание выполнено!