Никто не может :'( за 10 класс
Найдите точки минимума и максимума функции:
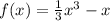
Другие вопросы по теме Алгебра
Популярные вопросы
- Впр 13 и 14 укр мова 10 клас Глазова...
3 - Определите словообразования: летчик-космонавт, мороженое (причаст.) мясо...
3 - Какие объекты можно одновременно рассматривать на двух уровнях организации...
2 - Слово дит’ясла яка частина мови?!?!...
2 - А.Какие препятствия преодолевал иван царевич в сказке царевна лягушка...
2 - Разложить на множители:1/8а²-а⁵...
1 - Питання до «Червоне і чорне» Хелпп 1. Про що мріяв Жульєн Сорель? 2....
3 - на кого распространяется административная, военная, духовная, родительская,...
1 - Дано: -5→а→-3. Оцінити значення виразу 1/a....
2 - 2 Put the verbs into Past Simple or Past Continuous. We (1. pack) our...
3
Определение локального максимума и локального минимума
Пусть функция
y
=
f
(
x
)
определена в некоторой
δ
-окрестности точки
x
0
,
где
δ
>
0.
Говорят, что функция
f
(
x
)
имеет локальный максимум в точке
x
0
,
если для всех точек
x
≠
x
0
,
принадлежащих окрестности
(
x
0
−
δ
,
x
0
+
δ
)
,
выполняется неравенство
f
(
x
)
≤
f
(
x
0
)
.
Если для всех точек
x
≠
x
0
из некоторой окрестности точки
x
0
выполняется строгое неравенство
f
(
x
)
<
f
(
x
0
)
,
то точка
x
0
является точкой строгого локального максимума.
Аналогично определяется локальный минимум функции
f
(
x
)
.
В этом случае для всех точек
x
≠
x
0
из
δ
-окрестности
(
x
0
−
δ
,
x
0
+
δ
)
точки
x
0
справедливо неравенство
f
(
x
)
≥
f
(
x
0
)
.
Соответственно, строгий локальный минимум описывается строгим неравенством