Неравенство с неизвестной степенью, корнем и логарифмом
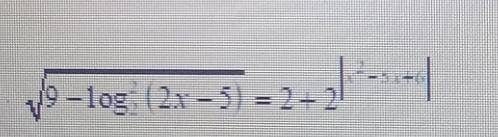
Другие вопросы по теме Алгебра
Популярные вопросы
- Семена у хвойных развиваются в семязачатках . почему же их называют голосеменными...
3 - Используйте распределительное свойство умнождения ,найдите значение выражений...
3 - Напишите не сочинение на тему за завтраком использую разноспрягательные...
1 - Какие функции выполняют системы внутренних органов паука...
2 - Один шофер перевиз самоскидом 560 ц цементу , а другий 490 ц.перший шофер...
1 - Как объяснить эти пословицы: ученье лучшее богатство.ученье-свет,неученье-тьма....
1 - Унашому класі 30 учнів, причому хлопців у 4 рази більше, ніж дівчат. скільки...
2 - 77..7777какой знак надо поставить чтобы равенство стало верным (но числа...
1 - Решите уравнения: а)3,5х-2,3х+3,8=4,28 б) (8,3-к)*4,7=5,64 в) 4,7у-(2,5у+12,4)=1,9...
2 - Какие лингвистические термины нужно знать по чтобы написать сочинение в...
1
(см. объяснение)
Объяснение:
Введем функции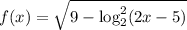 и
и 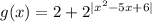 . Про вторую сразу скажем, что
. Про вторую сразу скажем, что 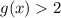 , но на этом не остановимся. Видим, что в степени у нас модуль, а значит самое маленькое, что мы можем получить - это
, но на этом не остановимся. Видим, что в степени у нас модуль, а значит самое маленькое, что мы можем получить - это 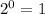 при
при 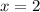 или
или 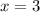 . Тогда наименьшее значение этой функции будет равно
. Тогда наименьшее значение этой функции будет равно 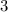 .
.
Теперь разберемся с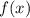 . У нас есть квадратный корень, поэтому все значения функции точно
. У нас есть квадратный корень, поэтому все значения функции точно 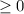 . Но и здесь мы идем дальше. Поменяем временно
. Но и здесь мы идем дальше. Поменяем временно 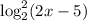 на букву
на букву 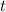 . Тогда будет
. Тогда будет 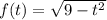 . Под корнем парабола, ветви которой направлены вниз, а значит есть наибольшее значение, равное
. Под корнем парабола, ветви которой направлены вниз, а значит есть наибольшее значение, равное 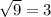 при
при 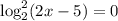 , откуда
, откуда 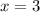 .
.
Наибольшее значение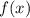 равно
равно 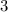 и достигается при
и достигается при 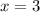 . Наименьшее значение
. Наименьшее значение 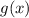 равно
равно 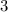 и достигается при
и достигается при 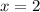 или
или 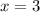 .
.
Тогда единственный корень исходного уравнения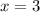 .
.
Уравнение решено!