Необходимо выполнить эти два задания. Заранее благодарю за

Ответы

MCKiri4PrO 15.10.2020 14:04

Наибольшая прибыль = 7 денежных единиц

Объяснение:

Пусть x - количество произведенной продукции П1, а y - количество произведенной продукции П2. Тогда цель задачи максимизировать значение (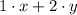 $1 \cdot x + 2 \cdot y$ ) при условии ограничений на сырье и того, что нам надо произвести хоть что-то: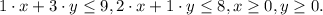 $1 \cdot x + 3 \cdot y \leq 9, 2 \cdot x + 1 \cdot y \leq 8, x\geq 0, y\geq 0.$

Эти четыре неравенства задают заштрихованный под прямыми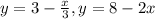 $y = 3 - \frac{x}{3}, y=8-2x$ четырехугольник в первом квадранте.

Значение максимизируемого выражения x+2y есть линии уровня z=x+2y, а так как градиент функции z(x,y) равный grad z = {1;2} направлен в сторону первого квадранта, то значения z будут тем больше, чем дальше мы продвинем линию уровня в первый квадрант. С учетом ограничений наибольшее значение изготовленной продукции придется на пересечение прямых, которые задают четырехугольник: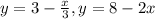 $y = 3 - \frac{x}{3}, y=8-2x$ . Точка пересечения (3;2). Значит, наибольшая прибыль, которую можно получить 3+2*2=7.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра