Необходимо найти среднее арифметическое корней уравнения. (вероятно решается через замену, но какую – не ясно)
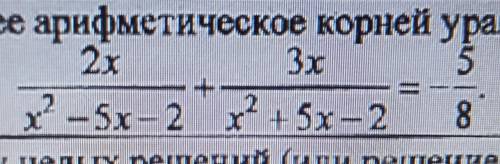
Другие вопросы по теме Алгебра
Популярные вопросы
- 1.) Составьте пищевую цепь, используя данные из текста (:подписав...
3 - Определите причинно-следственную связь исторических событий и запишите...
1 - Как вы оцениваете поступок Булата из произведения С.Жунусова «Штраф»?...
3 - Bookmark Әл -Фарабидің нақыл сөздеріЗадание №1Не сданоkeyboard_arrow_downӘл...
3 - Выпишите 1-2 предложения ,найдите и подчеркните грамматическую основу...
1 - Көмектесіңдерші кәзіркерек болып жатыр...
3 - Оқылым Мәтінді мұқият оқып, төмендегі тапсырмалардыорындаңыз. Әр...
2 - 1. Организм-прокариот: А) гриб лисичка В) лилия С) водоросль ламинария...
3 - Әдебиет Помагите ТЖБ надо закончить мәтін Хотя бы 4-5 сөйлем не...
2 - ответьте письменно на вопросы: 1. Зачем нужны модели? 2. Какова...
2
x^2-5x-2=a
x^2+5x-2=b
Тогда
b-a=10x
x=(b-a)/10
Подставляя
(b-a)/(5a) + (3*(b-a))/(10b) = -5/8
(b-a)*(1/(5a)+3/(10b)) = -5/8
(b-a)*(2b+3a)/(10ab) + 5/8 = 0
8(b-a)(2b+3a)+50ab = 0
8(8b^2+ab-3a^2)+50ab = 0
64b^2+8ab-24a^2+50ab = 0
64b^2+58ab-24a^2=0
2*(8b-3a)(4a+b)=0
1) 8b=3a
2) b=-4a
1) 8x^2+40x-16=3(x^2-5x-2)
2) x^2+5x-2=-4*(x^2-5x-2)
1) 5x^2+55x-10=0
2) 5x^2-15x-10=0
1) x^2+11x-2=0
2) x^2+3x-2=0
По теореме Виета
x1+x2+x3+x4/4 = (-11-3)/4 = -14/4 = -7/2