Не выполняя построения найдите координаты точек пересечения графика функции с осью х и осью у а)у=-х^2+4х+12
б)у=1/2 х^2+2
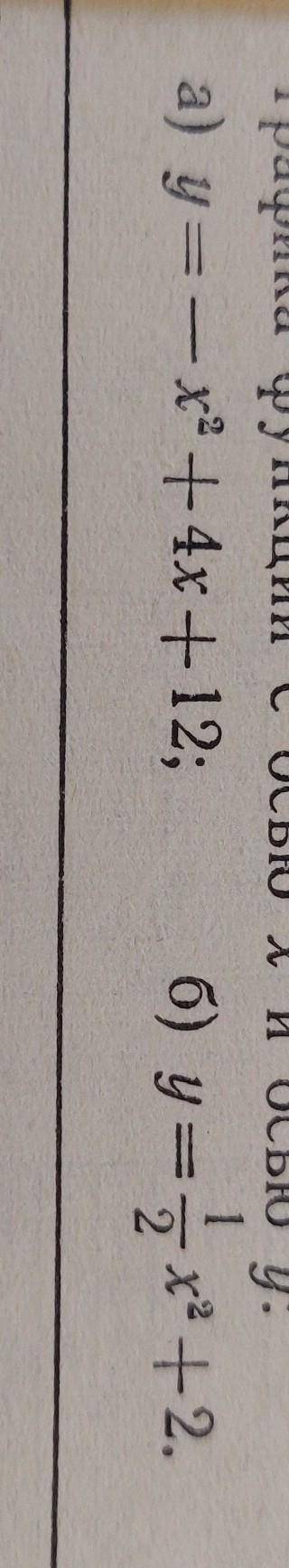
Другие вопросы по теме Алгебра
Популярные вопросы
- Как образовалась вся местность от урала до...
2 - Во сколько раз увеличится периметр квадрата, если его площадьувеличилась...
3 - Риса людського характеру, яка уславлюється у поемі гомера,, одісея,,...
3 - Составьте 20 реакций взаимодействия кислот и оснований...
1 - Сиет деген ақтамберді жыраудың шығармасына эссе жазу.50 сөз до...
2 - Выберите группу растений, плоды которых богатые . а) яблоня, вишня,...
3 - Втреугольнике mlp ml - биссектриса, ml = 28, lp = 12, mn-lp=18....
2 - Польза растений для моей жизни. эссе. 15б...
1 - Заполнить таблицу (как разные виды деревьев готовятся к зиме в...
2 - Як ви розумієте вислів-заклик знайти в собі шевченка ? ! ...
3
Точка пересечения с осью ОХ находится, если положить у=0 .
Точка пересечения с осью ОУ находится, если положить х=0 .
Нет точек пересечения с осью ОХ .
когда точка лежит на оси ох, ее ордината у=0, и наоборот, когда график пересекается с осью ох, ее абсцисса равна нулю. этим и воспользуемся.
а) с осью ох у=0; -х²+4х+12=0, по Виету х=6, х=-2; получили две точки пересечения с осью ох, это (6;0) ;(-2;0)
с осью оу х=0, у=12 одна точка (0;12)
аналогично б) с осью оу это точка, в которой х=0, т.е. (0;2) а вот с осью ох график этой функции не пересекается функция, 0≠((1/2)х²)+2 - как сумма неотрицательного числа ((1/2)х²) и положительной 2