1. Алгебра
  2. Не решая квадратного уравнения

Не решая квадратного уравнения 3x^2-x-11=0 a) найдите x1^2+x2^2 б) составьте уравнение с целыми коэфицентами,каждый корень которого на единицу больше соответствующего корня данного уравнения

0505levon 0505levon    2   21.05.2019 22:50    1

Ответы
мем23 мем23  01.10.2020 05:29

 

3x^2 - x - 11 = 0 \ | : 3\\\\ x^2 - \frac{1}{3}x - \frac{11}{3} = 0\\\\ x_1*x_2 = - \frac{11}{3}\\\\ x_1+x_2 = \frac{1}{3}

 

1) \ (x_1+x_2)^2 = x_1^2+2x_1x_2+x_2^2 = \frac{1}{9}\\\\ x_1^2-2(\frac{11}{3})+x_2^2 = \frac{1}{9}\\\\ x_1^2 + x_2^2 = \frac{1}{9}+\frac{22}{3} = \frac{1 + 66}{9} =\frac{67}{9}\\\\ 2) \ (x_1+1)(x_2+1) = x_1x_2 + x_1 + x_2 + 1 = - \frac{11}{3} + \frac{1}{3} + 1 = \\\\\frac{-11+1+3}{3} = -\frac{7}{3}

 

(x_1+1) + (x_2 + 1) = x_1 + x_2 + 2 = \frac{1}{3} + 2 = \frac{7}{3}\\\\ x^2 - \frac{7}{3}x -\frac{7}{3} = 0 \ | * 3\\\\ \underline{3x^2 - 7x - 7 = 0}

 

 

 

 

 

ПОКАЗАТЬ ОТВЕТЫ
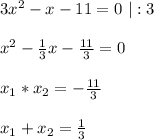
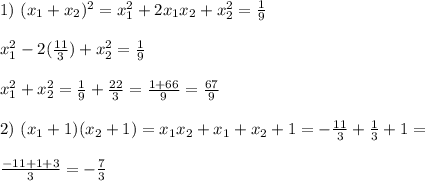
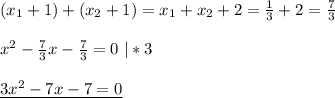
Другие вопросы по теме Алгебра
mmthe124 mmthe124  29.10.2020 02:43
a)Запишите область определения функции.b) Найдите множество значений функции. c) Определите промежутки знакопостоянства функции; d) Определите максимальное значение...
Criss666 Criss666  29.10.2020 02:43
Задача типа чертежа, как на картинке 6x+5/x-3 2...
крошкакартошка14 крошкакартошка14  29.10.2020 02:43
Знайти кут між прямими 3x - 2y + 5 = 0 і 2x - y + 2 = 0...
zFast88 zFast88  29.10.2020 02:51
Чи перпендикулярні прямі − 3x + 5y +1 = 0 і x + 2y + 2 = 0...
Ирина132435 Ирина132435  29.10.2020 02:51
Знайти рівняння прямої, що проходить через точку А(1;-2) і паралельна прямій 2x − 3y + 5 = 0...
ЕнотОбормот ЕнотОбормот  29.10.2020 03:03
Объясните, как мы получили вторую строчку. Желательно подробно весь пример расписать, как-никак . . Заранее большое...
Rose123456789 Rose123456789  29.10.2020 03:14
X^2-49/x+6≤0 С чертежом вроде такого)...
Angelochek1915 Angelochek1915  29.10.2020 03:39
Дано угол BOC-прямая угол2 равен 70°найти угол 1​...
strelchyksofia20005 strelchyksofia20005  29.10.2020 03:40
Выполните умножение распишите как сокращали и т. Д​...
taganrog123 taganrog123  29.10.2020 03:59
А) х5∙х12∙х3 Б) y13: y9 ​ 2.Представьте в виде произведения степеней степени. А) (ax)7 Б) (nm)15 ​ 3)Упростите выражение А) 2 а-2 ∙3а4 Б) 24 а6: (6а-3) ​ 4) Представьте...

Популярные вопросы