Найти значения a при которых уравнение ax^2+2x-3=0 имеет два различных корня

Ответы

РафикЖирафик 17.06.2020 05:01

ax^2+2x-3=0

Чтобы квадратное уравнение имело два различных корня, надо требовать выполнения двух условий: 1) a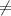 $\neq$ 0, 2) D>0.

D=4+12a.

Получим систему неравенств

$\left \{ {{a\neq0} \atop {4+12a0}} \right.$

$\left \{ {{a\neq0} \atop {12a-4}} \right.$

$\left \{ {{a\neq0} \atop {a-\frac{1}{3}}} \right.$

Отсюда при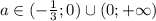 $a \in (-\frac{1}{3}; 0) \cup (0; +\infty)$ уравнение имеет два различных корня

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

kopachkirya03 06.09.2019 22:10

maruya3 06.09.2019 22:10

Исследовать и построить график функции у=х^3+3...

kseniya696969 06.09.2019 22:10

ekimmail631 06.09.2019 22:10

LeeAddon 06.09.2019 22:10

1) 3(4m-1)+4(7-2m) 2) (4x-3)(3x+2)-12x² 3) 5n(n²-2n)-2n(n²5n) 4) 15³-(3у²-2)(5y-1)...

Любаша5648 06.09.2019 22:10

RRuslan619 23.04.2020 17:58

steik20155 23.04.2020 17:58

Han121 23.04.2020 17:58

Последнее задание с решением...

krotkovaksenia1 23.04.2020 17:58

Скільки розв язків має рівняння -11=5х в кв.-7х...