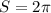Найти значение выражения  где s - сумма корней (или корень, если он один) уравнения
где s - сумма корней (или корень, если он один) уравнения = 4\pi(\pi-x) + x^{2} +\frac{\pi }{2})
Другие вопросы по теме Алгебра
Популярные вопросы
- Как кочевники развитию торговли...
1 - Прочитай текст. Определи основную мысль каждой части....
2 - 11. На протон, що влетів у магнітне поле перпендикулярно до ліній магнітної індукції,...
1 - На рисунку схематично показані зоря 3, планета П та її супутник С. Визначте графічно...
3 - 10. Уявіть, що у вірші замість слова «Якщо» неодноразово вжито слова «треба»,...
3 - Радіус основи конуса дорівнює 7 см, а висота конуса на 1 см менша від твірної....
2 - Період обертання диска по колу 20 с. Яка його частота обертання...
1 - 10 класс Углеводороды Вариант 2 1. Номенклатура УВ Назовите вещества, укажите...
2 - 1. Three, baby, ten, man, dark, not, woman, two, girl, number 2. are flowers....
2 - Тәуелсіздікке тақпақ керек ед отнееем комек керек...
2
Левая часть уравнения не больше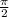 (поскольку арксинус принимает значения в промежутке
(поскольку арксинус принимает значения в промежутке ![\left[-\frac{\pi}{2};\frac{\pi}{2}\right]](/tpl/images/3210/9529/3b5e1.png) ), правая часть уравнения не меньше
), правая часть уравнения не меньше 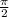 (поскольку равна сумме числа
(поскольку равна сумме числа 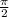 и квадрата, который, как известно, не бывает отрицательным). Поэтому обе части должны быть равны
и квадрата, который, как известно, не бывает отрицательным). Поэтому обе части должны быть равны 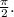 Откуда
Откуда 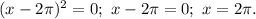 Подставляя полученное значение неизвестной в левую часть уравнения, убеждаемся, что и она в этой точке равна требуемому значению:
Подставляя полученное значение неизвестной в левую часть уравнения, убеждаемся, что и она в этой точке равна требуемому значению: 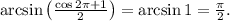
ответ: