1. Алгебра
  2. Найти значение многочлена

Найти значение многочлена f(x) от матрицы A. 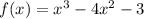f(x)=x^3-4x^2-3\\


A={3, -2, 2}\\\ {2, -1, 2}\\{2, -2, 3}

пжнужнапомощьмне пжнужнапомощьмне    3   09.01.2022 20:18    3

Ответы
agulmira62 agulmira62  09.01.2022 20:20

Можно просто подставить матрицу и вычислить значение <<в лоб>>. Однако можно и упростить себе жизнь: вычислим характеристический многочлен матрицы: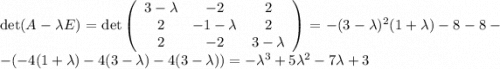 \det(A-\lambda E) = \det \left(\begin{array}{ccc}3-\lambda&-2&2\\2&-1-\lambda&2\\2&-2&3-\lambda\end{array}\right) = -(3-\lambda)^2(1+\lambda)-8-8 --(-4(1+\lambda)-4(3-\lambda)-4(3-\lambda)) = -\lambda^3+5\lambda^2-7\lambda+3.

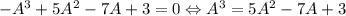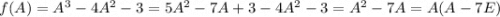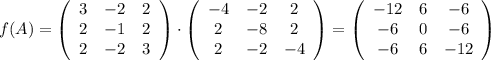Тогда по теореме Гамильтона-Кэли имеем: -A^3+5A^2-7A+3=0 \Leftrightarrow A^3 = 5A^2-7A+3, следовательно, f(A) = A^3-4A^2-3 = 5A^2-7A+3-4A^2-3 = A^2-7A = A(A-7E). Ну а это уже легко считается: f(A) = \left(\begin{array}{ccc}3&-2&2\\2&-1&2\\2&-2&3\end{array}\right)\cdot \left(\begin{array}{ccc}-4&-2&2\\2&-8&2\\2&-2&-4\end{array}\right) = \left(\begin{array}{ccc}-12&6&-6\\-6&0&-6\\-6&6&-12\end{array}\right).

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Мармеладик9 Мармеладик9  07.09.2020 13:21
Для яких значень х виконується умова f (х) 0 для функції, графік якої зобра- жений на рисунку і яка задана на проміжку -3; 3]?...
Ghannik08 Ghannik08  07.09.2020 13:22
4xy+xy^2-5x^2+y=08x^4y+5x^2y=11xy+xz+zy=1xyz-x^2-y^2-z^2=2...
ElvirO ElvirO  07.09.2020 13:57
решить задачу нарисовать функцию графига алгебра...
nastyabelgina1 nastyabelgina1  07.09.2020 13:22
Теңдеулер жүйесін алгебралық косу тасилимен шеш x-y=3 x-y=15​...
sadernik2 sadernik2  07.09.2020 13:26
Постройте графики уравнений а) х^2 +у^2 =16 б) (х-3)^2 +(у-1)^2 =9​...
Семён3228 Семён3228  07.09.2020 14:56
Біздің заманымыздаң 3000 жылдай бұрын ежелгі вавилон қолжазбаларында b2a сақталынған осы формуланың көмегімен санның квадрат түбірін жуықтап анықтайық 314=5,21..​...
2005161718 2005161718  07.09.2020 14:56
Может ли cos альфа принимать значение равное??...
vasa2283 vasa2283  07.09.2020 14:55
Докажите тождество (a-1+1/1-a)×a²-a/(2-a²)=a²/a-2​...
NEADgff NEADgff  07.09.2020 14:55
Найти область определения функции y=x^2 /4...
умник1622 умник1622  07.09.2020 14:55
Найди х из пропорции только четные...

Популярные вопросы