Найти значение функции, если tg (x)=2
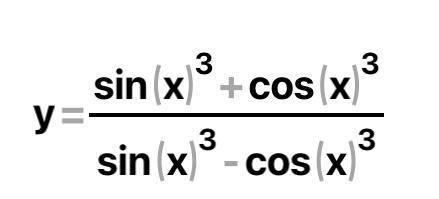
Другие вопросы по теме Алгебра
Популярные вопросы
- Водном подъезде нового дома 9 этажей, по 7 квартир на каждом этаже. заселены...
3 - Слово, которое обозначает легкий теплый ветер, и сладкое лакомство, и легкую...
3 - Решите систему неравенств х-4 0 3х в квадрате -15х 0...
1 - 30 сделать синтаксический разбор этих предложений=день кончался и приближались...
3 - Ветвь ели кажется гигантской рукой сделайте сколько тут глухих звуков и...
3 - Ессе на тему суров закон, но это закон...
3 - Футболка стоит 500рублей после снижения цены она стала стоит 390рублей на...
3 - Отгадайте загадку! в этом деле принимают участие 2 человека, когда они это...
1 - Середино океонические хребты являются границей между единственный океан...
1 - Решить только что добытый уголь соделжит 2÷ воды, затем он впитывает еще...
3
ответ:
Объяснение: очень надеюсь, что это синусы и косинусы в степенях, а не значение Х. Умножим числитель и знаменатель на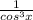 ;
;