Найти все значения a, при которых вершины парабол и лежат по разные стороны от прямой y=3/4
Другие вопросы по теме Алгебра
Популярные вопросы
- Написать о празднике guy fawkes...
1 - 90 . напишите в чем смысл высказывания и 2 аргумента (один из ) кто не прилагает...
2 - Y= [tex]y = \sqrt{12x + 5} [/tex]12x + 5...
3 - Читы 44 х 1/3 общие общие дробная черта 5 x 1/2 / 2 1/3 / 3 1/2 общее дробная...
3 - Число которое делится на 51 и 5...
2 - Надо завтра сдать! сочинение на тему особенности черт народа...
2 - Для полива огорода за готов или 200вёдер воды.на каждую грядку вылили по...
3 - 1) морфологический разбор приложения легкий морозец и покрывает лужицу...
3 - Подберите антоним к слову верный...
1 - Входе революции во франции была свергнута власть короля а) карла v b) людовика...
3
Координата х вершины параболы находится по формуле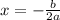 , тогда
, тогда 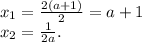
Условие при котором эти вершины лежат по разные сторны от прямой y=3/4 следующее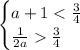 или
или 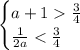
эти два условия можно объединить в одно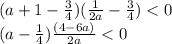
Полученное неравенство решим методом интервалов. Рисунок в прикрепленном файле.