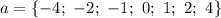Найти все значения а ,при которых уравнение ах^2 -(а^2+4)х+4а=0 имеет только целые корни
Другие вопросы по теме Алгебра
Популярные вопросы
- Определите виды придаточных!...
2 - Используя карту, выясните, на каких территориях по результатам реформы 1861 г....
1 - К588. Решите задачу алгебраи ческим. Один из углов треугольника в два раза меньше...
3 - Составьте и запишите рассказ на тему подготовка к встречи друзей...
2 - Найти угол ABC. С подробным решением...
2 - Чем творчество Л Н Толстого может быть интересно современному читателю план сложный...
1 - Знайти корені cosx = √2/2...
1 - А каком историческом периоде в жизни России идёт речь в рассказе Христова всенощная...
2 - Радіус кола,вписаного в трикутник ,дорівнює 3 см,а периметр трикутника дорівнює...
2 - Какие при к паразитизму имеют острицы и аскорида ...
2
Определим дискриминант данного уравнения при условии, что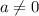 :
:
Найдем значения корней:
Первый корень будет целым, если будет целым.
будет целым.
Чтобы второй корень был целым, нужно найти общие делители числа 4: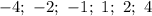
Решим уравнение, когда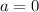
Объединяем все полученные ответы: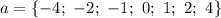
ответ: