1. Алгебра
  2. Найти все принадлежащие отрезку

Найти все принадлежащие отрезку [0 ; 2,5п]корни уравнения cosx=-√3/ 2 с двойного неравенства.

Dendizevs Dendizevs    3   30.09.2019 04:30    36

Ответы
Nikilengelo Nikilengelo  09.10.2020 04:37

\frac{5\pi }{6} ; \frac{7\pi }{6} .

Объяснение:

cosx =-\frac{\sqrt{3} }{2} ;\\\\x= \pm arccos (- \frac{\sqrt{3} }{2} ) +2\pi k, ~k\in\mathbb {Z};\\\\x=\pm \frac{5\pi }{6} +2\pi k, ~k\in\mathbb {Z};

Выберем корни уравнения . принадлежащие отрезку [ 0; 2,5\pi ]

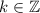0\leq \pm \frac{5\pi }{6} +2\pi k\leq \frac{5\pi }{2}|: \pi , ~k\in\mathbb {Z}\\\\0\leq \pm \frac{5}{6} +2k \leq \frac{5}{2} ,~k\in\mathbb {Z}

1)

\ 0\leq \frac{5}{6} +2k \leq \frac{5}{2} ;\\\\-\frac{5}{6} \leq 2k \leq \frac{5}{2} -\frac{5}{6};\\\\\- -\frac{5}{6} \leq 2k \leq \frac{5}{3} ;\\\\-\frac{5}{12} \leq k \leq \frac{5}{6} .

т.к. ~k\in\mathbb {Z} , то данному неравенству удовлетворяет  k=0

k= 0 , x = \frac{5\pi }{6}

2)

\ 0\leq -\frac{5}{6} +2k \leq \frac{5}{2} ;\\\\\frac{5}{6} \leq 2k \leq \frac{5}{2} +\frac{5}{6};\\\\\-\frac{5}{6} \leq 2k \leq \frac{10}{3} ;\\\\\frac{5}{12} \leq k \leq \frac{5}{3} .

данному неравенству удовлетворяет k=1

k=1, x= -\frac{5\pi }{6} +2\pi = \frac{-5\pi +12\pi }{6} = \frac{7\pi }{6} .

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
121ПЕРСИК121 121ПЕРСИК121  17.11.2020 12:43
4 задание Буду благодарен....
НАСТЯ7539 НАСТЯ7539  17.11.2020 12:43
8s3+2s2+12; 4s2−6s3 и s3−6s2−8, получаем... 1)7s3+4 2)4s3+4s2+4 3)3s3+4 4)13s3−2s2+4...
svetakurilova1 svetakurilova1  17.11.2020 12:43
быстрее сделайте лучше в тетрадке тк так надо и лучше будет за ранее спс...
Alinonik Alinonik  17.11.2020 12:43
Запишите формула (sin sin x)’=...
dima03102003 dima03102003  17.11.2020 12:43
Сегодняшние кочевые народы Найдите серию отдельных жирных слов.овца, казан, лук, крупный рогатый скотулица, караван, конь, верблюдюрты, верблюды, грузовики, козылуки, крупныйрогатый...
pomidorka334 pomidorka334  17.11.2020 12:44
В арифметич. прогрессии {an} известны значения двух её членов а10=261, а20=61. Найдите значение а16...
cocosobanro cocosobanro  20.11.2020 09:06
Тема: «Повторение темы: Функция y=k/x, ее график и свойства и функция y=kx2, ее график и свойства» 1) Самостоятельная работа.Постройте график функции и написать все его свойства:а)...
волшебство5 волшебство5  20.11.2020 09:06
Сколько будет log 2,5 по основанию 5 + log 2 по основанию 5...
кака231 кака231  20.11.2020 09:06
Найдите коэффициенты и дискриминант квадратного уравнения: 1) 3х² - 12х - 9 = 0;2) - x² – 12х +21= 0;3) 2 2/7х² - 1 2/7х - 1/7=0;4) -1,4х2 + 21х + 2,7 = 0;5) 2/9х² - 1 2/3х - 1/6=...
bauka077 bauka077  20.11.2020 09:06
1. Найдите значение выражения: 7² — 0,4 - 5³.​...

Популярные вопросы