Найти все пары простых чисел x и y , удовлетворяющих уравнению: x^2 - 2y^2 = 1

(3;2)

Объяснение:

Докажем  сначала, что если x и y - натуральные числа и удовлетворяют этому уравнению (кстати, это частный случай диофантова уравнения, которое называют уравнением Ферма или уравнением Пелля), то либо x либо y делятся на 3 (точнее, ровно одно из них делится на 3, но для нашего решения это не важно). В самом деле, если x и y не делятся на 3, то

то есть не может равняться 1. (число A получилось после вынесения общего множителя 3).

Итак, x или y делится на 3. Но по условию x и y - простые, поэтому x или y

равен 3.

1-й случай.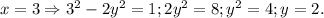

Поскольку 2 - простое число, получили решение (3;2).

2-й случай.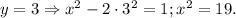

Такое уравнение не имеет решений в целых числах.

Объяснение:

Пусть   y = 2 , тогда  x² = 9  и  x = 3 , если x = 2 , то   2y² = 3  , а

полученное  уравнение решений  в натуральных числах  не

имеет , пусть x ≠ 2  и  y ≠2  , тогда x и y - нечетные  числа :    

x = 2k + 1  и  y = 2m + 1 , подставим эти выражения в исходное

 уравнение : 4k² +4k +1  - 2( 4m² + 4m + 1)  = 1

или : 4k²+ 4k -8m²-8m = 2  ⇒ 2( k²+k - 2m² -2m ) = 1  , но

полученное  уравнение не имеет решений в натуральных

числах , так как левая часть кратна 2  , а правая нет ⇒ ( 3  ; 2 )

 - единственная пара простых чисел , удовлетворяющая

исходному уравнению