Найти все корни уравнения cosx + (1 + cos x)tg^2x-1=0, удовлетворяющие неравенству tgx>0.
Другие вопросы по теме Алгебра
Популярные вопросы
- Почему пишется слитно, ведь глагол с не пишется всегда раздельно. нам...
1 - Расстояние 400км один поезд пришёл на час быстрее другого . какова...
1 - Замените отношения дробей отношением целых чисел : а)8целых6/7 : 17целых5/7...
3 - F(x)=2/x - 8/ sqrt x + 6/ 3sqrt x^2 + 2x + 6x^2 * sqrt x...
2 - Напишите сочинение на тему в зимнем лесу .! особено опираясь на то...
1 - Сравнительная характеристика пугачева и гринева. заранее !...
1 - Месторождения каких топливных ресурсов имеются в узбекистане?...
2 - Қандай себептің әсерінен тау жыныстары үгіледі? түсіндіріңдер және...
3 - Киялды,сары сайран,жуйрик откир,жас,билим,улттык,табигатк,ересек,жасоспорим...
2 - Что такое асбест 15 . по быстрей...
3
(см. объяснение)
Объяснение:
Попробуем решить это уравнение относительно тангенса:
Тогда получили два случая:
Применив формулу для тангенса половинного угла, получим:
Применив формулы суммы и разности тангенсов и выполнив очевидные преобразования, получим:
Решим каждое уравнение по отдельности:
1)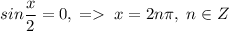
2)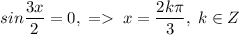
Окончательное решение уравнения с учетом ОДЗ:
Найдем теперь корни уравнения, которые удовлетворяют неравенству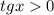 :
:
Задание выполнено!
Комментарий:
Замечу, что исходное уравнение можно упростить до вида:
Откуда хорошо видно, что его корень:
Такое решение также является допустимым.