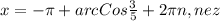Найти все корни этого уравнения, принадлежа- щие отрезку [0; 2].
Другие вопросы по теме Алгебра
Популярные вопросы
- Как и где греки узнали о возвращении независимости городам Эллады? Была...
3 - Названия животных последняя буква ь и в 3 склонение 5 слов хватит...
2 - С какой целью девушка приехала в город, где жил Юшка? В чем смысл ее жизни?...
2 - Нужно подсчитать адреса с подробностями. Количество подсетей = 2n, где...
2 - Який знак потрібно поставити між виразами:(–1)3 і –0,15 : 3...
2 - 70 км арақашықтығы жылдамдық пен уақыт...
3 - 1) Поставь глагол в настоящее время (мн. ч., 3 л.), образуй от него действительное...
2 - A1. Определите логику построения ряда и дополните его недостающим элементом:...
1 - В урне 5 белых и 3 черных шаров. а) Из урны вынимают одновременно два шара....
1 - За 4,2кг. Печенья заплатили 336 рублей. Сколько рублей надо заплатить за...
1
Если Сosx= - 3/5 , то Sinx = 4/5 или Sinx = - 4/5,так как Sin²x + Cos²x=1
Значит угол второй четверти синус которого равен 4/5 , а косинес которого равен - 3/5 не подходит .
ответ :