Найти все частные производные второго порядка функции двух
переменных:
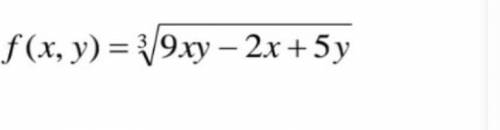
Другие вопросы по теме Алгебра
Популярные вопросы
- Вкаком агрегатном состоянии - газообразном жидком или твердом находится сера?...
2 - Запишите все натуральные числа,которые: а)больше 355 и меньше 362; б)больше 10...
3 - Сколько прямых можно построить через 4 точки. если можно с рисунком...
2 - Выразите величину в указанных единицах измерения: 1) 2 дм= мм 2) 5 м2= см2 3)...
2 - Возмущенный разбор слова по составу...
1 - Решить . за 4 часа теплоход км. за сколько часов он пройдет с той же скоростью...
1 - Такое сколько языков в нашей стране...
1 - Графики функций а) y=2(x/2 + 3)^2 б) y=3cos(3x+п/6)-2...
2 - На пошив платья ушло 2 целых 1/4 дня, а на отделку вышивкой- на 1/2 дня больше....
3 - Разобрать слова: гигантских,отложениями. мне нужен морфемный разбор...
1
Объяснение:
Сначала найдем производные первого порядка:
Теперь берем производные второго порядка: