1. Алгебра
  2. Найти угол наклона касательной

Найти угол наклона касательной к графику функции 1 - ( корень из трёх разделить на x) с абсциссов x0 = -1

mariakochmar mariakochmar    2   05.06.2019 13:00    0

Ответы
asya13051 asya13051  05.07.2020 23:50
Тангенс угла наклона касательной к графику функции с осью ОХ равен значению производной в точке касания. Поэтому:

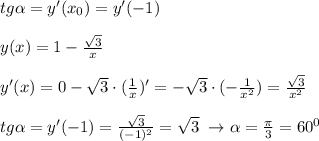
tg \alpha =y'(x_0)=y'(-1)\\\\y(x)=1-\frac{\sqrt3}{x}\\\\y'(x)=0-\sqrt3\cdot (\frac{1}{x})'=-\sqrt3\cdot (-\frac{1}{x^2})=\frac{\sqrt3}{x^2}\\\\tg \alpha =y'(-1)=\frac{\sqrt3}{(-1)^2}=\sqrt3\; \to \alpha =\frac{\pi}{3}=60^0
ПОКАЗАТЬ ОТВЕТЫ
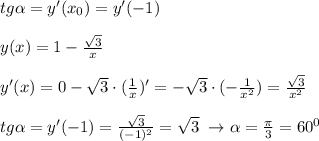
Другие вопросы по теме Алгебра
Nastya21724 Nastya21724  03.08.2019 21:10
Дали дробь со знаменателем (9+2)(9-2), скажите, как можно ?...
kisaayan kisaayan  03.08.2019 21:10
При каком значении t значение выражения 11-2t на 7 больше значения выражения 8t+24 ?...
lesanazyrova lesanazyrova  03.08.2019 21:10
Периметр равен 72 см,а одна из его сторон больше в 4 раза найдите все стороны...
artiom726 artiom726  17.07.2019 01:40
Дано уравнение 9z+(−0,7)9=(−0,487)8 ответь на вопросы: 1. какое число после возведения в степень отрицательное? (выбери верный ответ) (−0,7)9 (−0,487)8 2. какое число...
ЛимАнель ЛимАнель  17.07.2019 01:40
Какую из дробей нельзя представить в виде периодической? а) 2\3 б) 3\4 в) 5\6 г) 6\7...
diana2005n diana2005n  17.07.2019 01:40
При каких значениях х выражение 7 делённое на х во 2 степени -9,имеет смысл? ; -3) ; -3) u (3; +бесконечность) ; -3) u (-3; 3) u(3; +бесконечность) г)(3; +бесконечность)...
serditex89041361 serditex89041361  17.07.2019 01:40
Решите уравнение : log x 36= 2; log x дробь 1,27= -3...
danilf999 danilf999  17.07.2019 01:40
Моторная лодка километров по течению реки и 42 км против течения за то же время за находится километров стоячей воде найдите скорость лодки в стоячей воде если скорость...
LenaFox456 LenaFox456  17.07.2019 01:40
Путь от одной станции до другой товарный поезд дошел за 8 часов, а поссажирский за 5 часов. если скорость пассажирского поезда равна 80 км/час, то скорость товарного...
Milky0405 Milky0405  17.07.2019 01:40
Выполните умножение: 49а^2-в^2\8а^2*а\14а-2в...

Популярные вопросы