найти угловой коэффициент касательной к графику функции y=ln(2x+1) в точке x0=2
Другие вопросы по теме Алгебра
Популярные вопросы
- Будьте добры, ! log по основанию 1/3 числа (5-2x) = -3...
3 - Вшапке-невидимке слово, место для него готово. шапку эту надо снять,...
1 - Найти точку минимума функции y=-1/x-x...
1 - Возведите данное выражение в степень: а)(2х) в пятой степени; б)(10х...
3 - Первая труба пропускает на 4 литра воды в минуту меньше чем вторая...
2 - Выразите из равенства каждую переменную через другую: a-d-c=0 выразить:...
3 - Чему равно 84, если 8 × 8 = 54? чему равно 100, когда 5 × 6 = 33?...
3 - Ctg(arccos1+arctg(- корень из 3/3))...
1 - Через данную точку проведите прямую пересекающую две данные прямые...
1 - Сочинение по на тему если б не было силы трения...
1
По геометрическому смыслу производной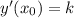
ответ: 0,4.