Найти точки экстремума функции .

Объяснение:

Данная функция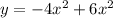 является квадратичной функцией (многочлен второй степени) и задаёт квадратичную параболу. Как известно, у такой функции может быть лишь один экстремум, находящийся в вершине параболы.

Упростим исходную функцию: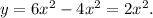

Для нахождения единственного экстремума воспользуемся производной: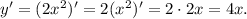

По лемме Ферма, значение производной от экстремума нулевое. Таким образом, точки экстремума будет решением .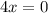

Для нахождения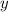 точки экстремума вычислим значение исходной функции от найденного :

Получается, что координаты точки экстремума это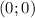 .