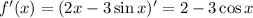Найти тангенс угла наклона касательной к графику функций f(x) в точке x f(x)=3x^2-12+5. x=-1 f(x)= 4cosx+x. x=π/6 f(x)= 2x^2+8x-3. x=-3 f(x)=2x-3sinx. x=π π(пи)
Другие вопросы по теме Алгебра
Популярные вопросы
- Задание 2. ( ) Решите неравенство: 3(х – 1) 5x – 3...
2 - 3. Запишите следующие формулы на языке программирования:a-b:c=5-a:b+c=2ax...
3 - используя деление уголком, запишите в каноническом виде частное при...
3 - ответьте на вопросы по произведению Петька на даче : Какие чувства...
1 - зная что 728×5609-4 083 352,найди правильные ответы.из соответствующих...
3 - 2 сөйлем асырмслы по английскискому...
1 - коля с друзьями играли в футбол 1 час 20мин 2/5 этого времени они...
1 - решите уравнение (х-2)(х-3)(х-3)(х-4)=20 ,в ответе указать количество...
2 - Развитие капиталистических отношений в Казахстане. Урок 1 Выбери правильный...
2 - Решите уравнение и найдите все его корни (x-1)x(x+1)(x+2)=24. В ответе...
1
Геометрический смысл производной. Производная в точке x0 равна угловому коэффициенту касательной к графику функции y=f(x) в этой точке
в первом опечатка, скорее всего f(x) = 3x^2 - 12x + 5.
Найдем производную функции:
2) Аналогично, производная:
3) Производная функции:
4) Производная функции: