1. Алгебра
  2. Найти сумму первых 10 членов прогрессий

Найти сумму первых 10 членов прогрессий


Найти сумму первых 10 членов прогрессий

Lera2010K Lera2010K    3   13.01.2022 05:05    0

Ответы
khfozilzhonov khfozilzhonov  13.01.2022 06:00

ответ:  C) .

\{b_{n}\}:\ \ \sqrt6\ ,\ 3\sqrt2\ ,\ 3\sqrt6\ ,\ ...

Проверим, является ли эта последовательность геометрической прогрессией. Если отношение каждого последующего члена к предыдущему одинаково, то последовательность  является геометрической прогрессией.

\dfrac{b_2}{b_1}=\dfrac{3\sqrt2}{\sqrt6}=\dfrac{3\sqrt2}{\sqrt3\cdot \sqrt2}=\dfrac{3}{\sqrt3}=\sqrt3dfrac{b_3}{b_2}=\dfrac{3\sqrt6}{3\sqrt2}=\dfrac{\sqrt6}{\sqrt2}=\dfrac{\sqrt3\cdot \sqrt2}{\sqrt2}=\sqrt3

Последовательность  является геометрической прогрессией  и  знаменатель прогрессии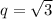  q=\sqrt3  .

\boxed{\ S_{n}=\dfrac{b_1(q^{n}-1)}{q-1}\ }\ \ \Rightarrow \ \ \ S_{10}=\dfrac{\sqrt6\cdot (\, (\sqrt3)^{10}-1)}{\sqrt3-1}=\dfrac{\sqrt6\cdot (3^5-1)}{\sqrt3-1}==\dfrac{\sqrt6\cdot (243-1)}{\sqrt3-1}=\dfrac{\sqrt6\cdot 242}{\sqrt3-1}=\dfrac{\sqrt6\cdot 242\cdot (\sqrt3+1)}{(\sqrt3-1)(\sqrt3+1)}=\dfrac{\sqrt6\cdot 242\cdot (\sqrt3+1)}{3-1}==121\, (\sqrt{6\cdot 3}+\sqrt6)=121\, (\sqrt{9\cdot 2}+\sqrt6)=\boxed{\ 121\, (3\sqrt2+\sqrt6)\ }

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
ekaterina7201 ekaterina7201  25.09.2019 06:40
Изначально у буратино и мальвины было поровну монет по 1 сольдо. буратино израсходовал в 9 раз меньше монет, чем мальвина, а осталось у него в 10 раз больше монет, чем у мальвины....
sveta6729 sveta6729  25.09.2019 06:50
Решите систему уравнений: 4х - у = 10,x+3y=-3...
SashaNemur SashaNemur  25.09.2019 06:50
При каком значении двучлена у-6 равняется значению трехчлена у в квадрате - 9у+3 ? в ответе запишите суму корней...
danisdigger danisdigger  25.09.2019 06:50
При каком значении д уравнение 2х в квадрате + 4х-д=0 имеет единый корень...
Dryunya1989 Dryunya1989  25.09.2019 06:50
Чему равна сумма корней 2х в квадрате -4х-5=0...
Тжвик Тжвик  01.04.2019 22:20
Для функции y=f(x) найдите первообразную: f(x)= -1/(6x+1)^2...
krikunnik krikunnik  01.04.2019 22:20
Для некоторой арифметической пргресии выполняется следущее равенство : а2 + а4 ++а60-(а1 + а3 ++а59)=90 найдите разность этой прогрессии. )...
Шпунтик99 Шпунтик99  01.04.2019 22:20
Докажите, что при любом нечетном значении m значение многочлена m³ - m делится на 24....
Аполлинарияполишка Аполлинарияполишка  01.04.2019 22:20
Вычислите 4/3 во 2 степени умножить 0,5 во второй степени и разделить на 2/9 в 3 степени...
Машуник1 Машуник1  01.04.2019 22:30
Найдите квадрат суммы чисел 154 и 246...

Популярные вопросы