Найти сумму корней уравнения: 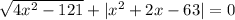. Я в вас верю, товарищи!

√(4x² - 121) + |x² + 2x - 63| = 0

товарищ верь ! взойдет она, звезда пленительного счастья напишут наши имена.

Слева 2 неотрицательных слагаемых . значит сумма равна 0, только тогда когда

√(4x² - 121) = 0 и  |x² + 2x - 63|  = 0

ищем корни

x² + 2x - 63 = 0

D = 4 + 4*63 =  256 = 16²

x12 = (-2 +- 16)/2 = -9   7

Сравним с другими корнями

4x² - 121 = 0

x² = 121/4

x12 = +- 11/2

корни не совпадают

значит сумма всегда не равна 0

корней нет

решений нет

вот если

Вместо √(4x² - 121) было бы √(4x² - 144) то корень x = +- 7 сумма 7, а было бы √(4x² - 324) то корень х = +- 9 сумма -9