1. Алгебра
  2. Найти сумму действительных

Найти сумму действительных корней уравнения: x^4-2x^2-12x-8=0

даша3635 даша3635    1   02.03.2019 07:30    2

Ответы
gshsjtzjts gshsjtzjts  23.05.2020 21:17

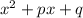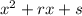Используем метод неопределённых коэффициентов.Предположим, что левая часть уравнения разлагается на множители второй степени с целыми коэффициентами. Обозначим один из них черезx^2+px+q , другой - через x^2+rx+s.

Задача сводится к нахождению p, q, r, s. Тогда

x^4-2x^2-12x-8=(x^2+px+q)(x^2+rx+s)=0

\begin{cases} p+r=0\\q+s+pr=-2\\ps+qr=-12\\qs=-8 \end{cases}

Можно попробовать взять q=4, s=-2, тогда p=2, r=-2, а уравнение может быть представлено в виде:

 x^4-2x^2-12x-8=(x^2+2x+4)(x^2-2x-2)=0

x^2+2x+4=0  не имеет действительных корней, так как дискриминант меньше 0 (2^2-4*4=-12).

x^2-2x-2=0

x_1=(2+\sqrt{12})/2=1+\sqrt{3}

x_2=(2-\sqrt{12})/2=1-\sqrt{3}

Сумма корней: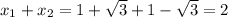 x_1+x_2=1+\sqrt{3}+1-\sqrt{3}=2

если взять q=-4, s=2, тогда p=-2, r=2, а уравнение может быть представлено в виде:

x^4-2x^2-12x-8=(x^2-2x-4)(x^2+2x+2)=0

x^2-2x-4=0

x_1=(2+\sqrt{20})/2=1+\sqrt{5}

x_2=(2-\sqrt{20})/2=1-\sqrt{5}

x^2+2x+2=0 не имеет действительных корней, так как дискриминант меньше 0 (2^2-4*2=-4).

Сумма корней: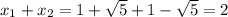 x_1+x_2=1+\sqrt{5}+1-\sqrt{5}=2

ответ: 2.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Aleksandra20061 Aleksandra20061  06.06.2019 13:40
Решить уровнение уровнения коэффицентов x-2y=8 x-3y=6 2x-3y=10 x-2y=-9 8x+3y=-21 4x+5y=-7...
Azadamurshaeva Azadamurshaeva  06.06.2019 13:40
Решите неравенство 3( х-1) больше 2(3- х...
voloseikotatian voloseikotatian  06.06.2019 13:40
Разложите на множители a^3+a^2-4ab-8b^3+4b^2...
lecsika lecsika  06.06.2019 13:40
Найдите все двузначные числа, сумма цифр которых не меняется при умножение на любое однозначное число, при этом цифра десятков больше цифры единиц...
di23di di23di  06.06.2019 13:40
На соревнования приехал 21 участник, из которых 2 друга, после всех участников разделили на 3 группы поровну, какова вероятность того, что 2 друга окажутся в одной команде?...
nik7748 nik7748  06.06.2019 13:40
Найдите координаты вектора b коллинеарному вектору а (4; -3) если a·b=75...
nebylobyagjjhgf nebylobyagjjhgf  06.06.2019 13:40
Представьте выражение (3b-5)*(3b+5) в виде многочлена. (решение и ответ ! )...
irinakarimova2 irinakarimova2  06.06.2019 13:40
Сумма отрецательных корней уравнения=? x^3+x^2-9x-9=0...
lizza3429 lizza3429  06.06.2019 13:40
Log2(2x-3)-log2(3x-5)=0 2 в основании...
hdjddngddh hdjddngddh  13.06.2019 15:10
Решить г)1/3*(0,216: 0,2-0,12*10) ж)0,3-4,2: (2,25-1целая7/8* 3целых1/3)...

Популярные вопросы