1. Алгебра
  2. Найти сумму целых решений

Найти сумму целых решений неравенства 5(x-1)\ \textgreater \ (x-1)^{2}

Den4ikBLeT Den4ikBLeT    3   05.10.2019 18:40    1

Ответы
поорд поорд  17.08.2020 08:46

5(x-1)(x-1)^2

5(x-1)-(x-1)^20

5x-5-(x^2-2x+1)0

5x-5-x^2+2x-10

-x^2+7x-60

Разделим обе части на (-1) и поменяем знак неравенства на противоположный:

x^2-7x+6

По теореме Виета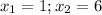  x_1=1;x_2=6

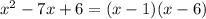
=> x^2-7x+6=(x-1)(x-6)

=(x-1)*(x-6)

Используя метод интервалов, получим решение данного неравенства:

1

Целые решения: 2; 3; 4; 5.

2+3+4+5 = 14  это и есть сумма целых решений неравенства.

ответ: 14.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Radmula Radmula  21.10.2020 21:08
Решить Контрольная работа по обществознанию за 1 четверть 7 класс I вариант Часть 1 1. Ученики 7 класса отвечали на вопрос: «Какую роль выполняют правила в жизни людей?» Один из...
вика8914 вика8914  21.10.2020 21:06
Число 12 _ дільник числа 240?...
NAPAS228 NAPAS228  21.10.2020 21:06
КАК ЭТО ДЕЛАТЬ???! Не пишите за »...
daryachita daryachita  21.10.2020 21:05
Разложите на множители: 7x -7y +tx -ty​...
JHopeЧонХосочек JHopeЧонХосочек  21.10.2020 21:05
I Вариант. Либо II вариант, какой вам легче и понятнее такой и делайте...
пучкаек пучкаек  13.03.2021 12:47
9/22 это правильная дробь или нет​...
plsplizovich plsplizovich  13.03.2021 12:45
0*(473747484*7474848626)=?...
Dhgfhdudv Dhgfhdudv  13.03.2021 12:45
Я хочу проверить своё решение где убывающая или возрастающая функуия y=(квадратный корень 7)^x, y=(2/квадратный корень7)^x, y=(3-квадратный корень 8)^x, y=1/(3-квадратный корень8)^x​...
katerinalavrenchuk katerinalavrenchuk  13.03.2021 12:45
Упрости выражение. (5,4x+19y)−(18x+8,6y) = x я знаю что это никто не зделает я смирился если хотите то я дам лучший ответ...
кек903 кек903  13.03.2021 12:44
В результате взвешиваний портфеля первоклассника был получен ряд (в кг): 3,3; 1,85; 2,2; 2,35; 1,7; 3,2; 4,4; 2,1; 3,4; 2,8.Заполните таблицу:Масса портфеляЧастотаНакопленная частотаОт...

Популярные вопросы