1. Алгебра
  2. Найти сумму бесконечно убывающей

Найти сумму бесконечно убывающей прогрессии если: q=, b₄= подробно, !

juliakovta juliakovta    1   07.07.2019 00:20    0

Ответы
Zzzzzzzzz1111 Zzzzzzzzz1111  30.07.2020 01:50
Формула суммы бесконечно убывающей геом. прогресии: 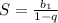S= \frac{b_1}{1-q} .

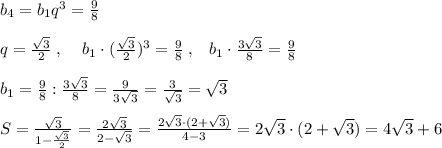
b_4=b_1q^3=\frac{9}{8}\\\\q= \frac{\sqrt3}{2} \; ,\; \; \; \; b_1\cdot (\frac{\sqrt3}{2})^3=\frac{9}{8}\; ,\; \; \; b_1\cdot \frac{3\sqrt3}{8}=\frac{9}{8}\\\\b_1=\frac{9}{8}:\frac{3\sqrt3}{8}=\frac{9}{3\sqrt3}=\frac{3}{\sqrt3}=\sqrt3\\\\S= \frac{\sqrt3}{1-\frac{\sqrt3}{2}} =\frac{2\sqrt3}{2-\sqrt3}=\frac{2\sqrt3\cdot (2+\sqrt3)}{4-3}=2\sqrt3\cdot (2+\sqrt3)=4\sqrt3+6
ПОКАЗАТЬ ОТВЕТЫ
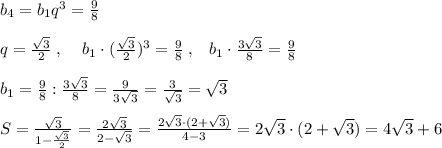
Другие вопросы по теме Алгебра
katyayatakozwmp5 katyayatakozwmp5  10.06.2019 14:40
Решить 1/3+0,3; 3/5-0,76; -1/6-0,5; 3/20-0,95...
kadalsu4 kadalsu4  10.06.2019 14:40
Вычислить: 10-5корень3 делённое на 10+5корень3 +10+5корень3 делённое на 10-5 корень...
davleeva davleeva  10.06.2019 14:40
Пусть x=-1\8 и y = 0,5 найдите значение каждого из выражений -(х+y); -(x-y); +y); -y) ! )...
muzaka muzaka  10.06.2019 13:48
Выручайте! без вас никак! разобраться в теме, я нахожусь на контрольной, нужно ! решите и подробно распишите! быстрее! желательно все, точнее умоляю все решить! надеюсь на...
HET228 HET228  10.06.2019 13:45
Dabc – тетраэдр. ас -ав - х -cd . тогда х = … 1) dа ; 2) вс ; 3) dв .обьясните...
МорскойКот МорскойКот  05.10.2019 19:00
1. знайдіть кут с трикутника авс ,заданого координатами його вершин: а(1; 1; 0), в(2; -1; 3), с(4; 1; 1).2.знайдіть суму координат точки перетину графіків функцій: y=3^x i...
dimon4ikk122 dimon4ikk122  05.10.2019 19:00
Знайдіть область визначення функції [tex]y = \frac{ \sqrt{4 - x} }{ x} [/tex]...
даша3549 даша3549  05.10.2019 18:50
Вычислить площадь фигуры, ограниченной кривымиy=e^x,y=e^-x,x=1...
пОмО0гите пОмО0гите  05.10.2019 18:50
На отрезке ав есть точка р.найдите суму средин ар и рв ,если ав=40 см ,,20...
NerminJaleÇiçek NerminJaleÇiçek  05.10.2019 18:50
Спроблемой. найдите уравнения прямой, которая параллельна прямой 4-9х=0 и проходит через точку м(6; 4)....

Популярные вопросы