1. Алгебра
  2. Найти сумму бесконечно убывающей

Найти сумму бесконечно убывающей прогрессии
1) 6, 1, 1/;
2) -25, -5, -1,

ника2763 ника2763    1   06.11.2019 01:40    1

Ответы
alenajad alenajad  10.10.2020 11:28

Сумма бесконечно убывающей геометрической прогрессии вычисляется по формуле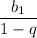 \dfrac{b_1}{1-q}.

Первая прогрессия

b_1=6

Найдём знаменатель прогрессии:

q=b_2/b_1=1/6

Теперь найдём сумму:

S=\dfrac{6}{1-1/6}=\dfrac{6}{5/6}=6 \cdot \dfrac{6}{5}=\dfrac{36}{5}=7\dfrac{1}{5}=7{,}2.

Вторая прогрессия

b_1=-25\\q=b_2/b_1=-5/(-25)=1/5\\S=\dfrac{25}{1-1/5}=\dfrac{25}{4/5}=25 \cdot \dfrac{5}{4}=\dfrac{125}{4}=31\dfrac{1}{4}=31{,}25

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
lightningwhite lightningwhite  16.12.2021 19:03
4. Каким может быть наибольший диаметр стола (в см), если для комфортного перемещения по комнате расстояние между столом и другими предметами мебели (расстояние между ближайшими...
1234567891155 1234567891155  16.12.2021 19:04
(4) Математика (Линейная и векторная алгебра полное решение. И, если применимо, объяснение ваших действий. Иначе, увы, не смогу принять вашу работу. Буду добавлять одинаковые задачи...
Ella003 Ella003  16.12.2021 19:05
A) (7-10)(x + 5) = 0; б) (a-5)(10a^2+3a)=0в) x^3+x^2-4x-4=0 До іть розв язати рівняння...
sofia200000 sofia200000  16.12.2021 19:05
Математика (Линейная и векторная алгебра полное решение. И, если применимо, объяснение ваших действий. Иначе, увы, не смогу принять вашу работу. Буду добавлять одинаковые задачи...
Miku1111 Miku1111  16.12.2021 19:06
Выполнить действия 1) 3х(х^4-5х+2) 2) (а-6) (а+7) 3) (4х+9)-(8х+12)...
azatnacu azatnacu  16.12.2021 19:06
Математика (Линейная и векторная алгебра полное решение. И, если применимо, объяснение ваших действий. Иначе, увы, не смогу принять вашу работу. Буду добавлять одинаковые задачи...
TATAP2004 TATAP2004  16.12.2021 19:06
(4) Математика (Линейная и векторная алгебра полное решение. И, если применимо, объяснение ваших действий. Иначе, увы, не смогу принять вашу работу. Буду добавлять одинаковые задачи...
Катя388891 Катя388891  16.12.2021 19:07
Упростите выражения 1) (x^2-1)3x-(x^2-2)2x 2) (4a^2-3b)2b-(3a^2-4b)3b 3) 2(3a+4)+3(a-7)-7(2a-7) 4) 3(2x-1)-5(x-3)+6(3x-4)...
mgvzvit2005 mgvzvit2005  16.06.2019 00:30
Решение квадратного уравнения х2-20х=-5х-13-х2...
MrEdgik MrEdgik  16.06.2019 00:30
Каково взаимное расположение графиков функций y=-27x-33 и y=27x+75 в случае пересечения графиков найдите координаты точки их пересечения.? !...

Популярные вопросы