Найти sin a и tg a, если cos=-√5/4, pi/2
Ответы
Угол второй четверти значит Sinα > 0 .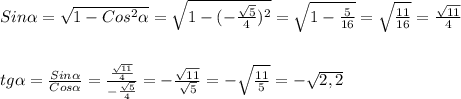
ПОКАЗАТЬ ОТВЕТЫ
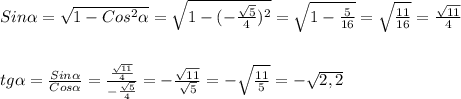
Другие вопросы по теме Алгебра
Популярные вопросы
- В году в нашем районе построили 12 новых домов, а в этом году — на 3 дома...
3 - В первом из новых домов 35 квартир, во втором на 20 квартир меньше, а в...
1 - Замени суммой одинаковых слагаемых числа 6, 8, 12, 16. Образец: 6 = 3 +...
2 - Выбери все высказывания, верные для этого рисунка: 1) Все флажки красного...
3 - Составь задачу по выражению и реши её. 1) 36+ (36-8) 2) 36+ (36+ 8)...
3 - В автобусном парке было 90 автобусов. Утром выехало в рейсы 50 больших...
1 - Утром в магазине было 30 шкафов для книг и 10 шкафов для одежды. К концу...
2 - Дети играли в слова. Аня назвала 30 слов, Ира — 25 слов, а Саша — на 20...
3 - В школе 100 второклассников. На экскурсию в музей поехали 25 учеников,...
2 - Купили две лампочки по 20 р. и фонарик за 50 р. Какова стоимость покупки?...
1