Найти решение дифференциального уравнения с разделяющимися переменными 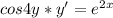
Другие вопросы по теме Алгебра
Популярные вопросы
- Алгебра 8 класс, Пожайлуста если знаете умоляю (...
2 - 7. Синонимдерді табыңыз а) сұлу,жақсы в) момын, кекшіл с) көмек, көмекші д) мереке,мейрам8....
2 - Диаметр шара равен 26 расстояние от центра до шара его сечения равно 5. Найдите...
2 - Бегун и велосипедист тренируются на круговой дорожке в парке. Когда они двигаются...
2 - синквейн на одного героя из рассказа лошадиная фамилия...
2 - 2) Як вивести палітру кольорів на екран? 3) Якими можливо розмістити декілька відкритих...
1 - 2. Изобразите на координатной прямой и запишите пересечение и объединение числовых...
3 - JA tпередвигаютсяорганические вещества.4. Транспорт кислорода и питательных веществ,...
1 - Задание 2. Напишите письмо современному Митрофанушке. В своем письме расскажите...
2 - Хелп надо В столбик ! 6 не надо ...
1
общее решение