Найти промежутки снижения функции
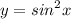
Другие вопросы по теме Алгебра
Популярные вопросы
- Определите порядок слов в предложениях, измените его на противоположный....
2 - Ккакому стилю речи относиться этот отрывок: в хозяйствах, в среде аграрников...
1 - 1)корень 15- 2х= 3 2) (1/8 ) в степени -3х = 32 помлгите решить !...
2 - Какой эпизод вам понравился в рассказе а.п.чехова смерть чиновника...
2 - Радиус основания конуса равен 5см а образуюшая конуса равна 13см найдите...
2 - На чемпионате по прыжкам в воду выступают 40 спортсменов среди них 4 прыгуна...
1 - Из за чего раскольников покушается на жизнь старухи - процентщицы...
1 - Перевести ! ! , меня зовут иван, и я хотел бы рассказать о своей семье....
1 - Вфирме такси в данный момент свободно 30 машин: 6 чёрных 3жёлтых и 21...
3 - Длина телескопички 5 м а длина лески до поплавка 3 м на каком расстоянии...
1
(1-cos2x)/2=(1-cos²x+sin²x)/2=sin²x
Вместо функции у=sin²x рассмотрим функцию у=(1-cos2x)/2, найдем ее производную. у'=sin2x
Нас интересуют промежутки убывания, т.е. те, где у'≤0, для этого решим неравенство
sin2x≤0;
-π-arcsin0+2πn≤2х≤arcsin0+2πn ; n∈Z;
-π+2πn≤2х≤2πn ; n∈Z;
-π/2+πn≤х≤πn ; n∈Z;
ответ
х∈[ -π/2+πn; πn] ; n∈Z
Функция убывает в тех промежутках, в которых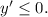
Функция убывает при![x\in \Big[\, -\dfrac{\pi}{2}+\pi n\ ;\ \pi n\ \Big]\ \ ,\ n\in Z\ .](/tpl/images/4738/3116/bcac0.png)