Найти производные данных функций:
Другие вопросы по теме Алгебра
Популярные вопросы
- Продолжите предложения, используя союзы и союзные слова, данные в скобках....
2 - Из текста рубрики «Знайте и применяйте!» (см. выше) выпишите все примеры и...
2 - Запишите сложноподчинённые предложения, соблюдая орфографические и пунктуационные...
1 - Используя материалы предыдущего упражнения, расскажите об основных отличиях...
3 - Спишите предложения, подчеркните грамматические основы, составьте схемы. 1)...
1 - Преобразуйте сложносочинённые предложения в сложноподчинённые. Сравните синтаксические...
1 - Установите, в чём сходство и в чём различие данных предложений. Составьте...
3 - Продолжите предложения так, чтобы они получились сложноподчинёнными. Составьте...
1 - Спишите, раскрывая скобки, вставляя пропущенные буквы и знаки препинания....
2 - Спишите предложения, раскрывая скобки, вставляя пропущенные буквы и знаки...
2
=============================
Объяснение:
Объяснение:
Сложная функция вида: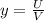
Тогда производная будет выглядеть следующим образом:
Преобразуем: