Найти производные 3 функций 1) y=6/x+1/2x^2-3/корень из x 2)y=cos(1+корень из x -x^2) 3) y=7^cos2x
Другие вопросы по теме Алгебра
Популярные вопросы
- Твір роздум на тему з чого зроблені крила людини нужно...
3 - Сравни: a a+6. b b-5 c+7 7+c...
3 - 2. Обозначьте орфограмму «е, и в окончаниях существительных». I, к рекеразноскл.на...
3 - Укажите причастие в суффиксе которого пишется а(я) А стро...щийся Б бор...щийся...
3 - ЗАРУБЕЖНАЯ ЛИТЕРАТУРА!2 складні ситуации з життя Тома Сойєра и Полианны...
3 - 877. Выполните действия: 1) 10,5:15+1,8; 3) 46,2 : 132.1,6;2) 67,2:12-3,25;...
1 - Кто свою мать, чужую Как полная пословица выглядит?...
1 - Із двох станцій назустріч один одному виїхали два поїзди. Один їхав зі...
1 - Решите это всё Задание на фото! ...
2 - Решить систему неравенств: 1.{█(3+2x [email protected]+2x -1)┤ 2.{█(0,5x...
2
1)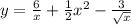
2)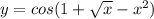
3)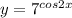
1) -6/x^2+4x^2/2x^4-3/2корня из x
2) -sin(1+корень из x -x^2)+1/2корня из x-2x)
3) 7^cos^2-sin^2=7^-sin2-cos2