Найти производную второго порядка
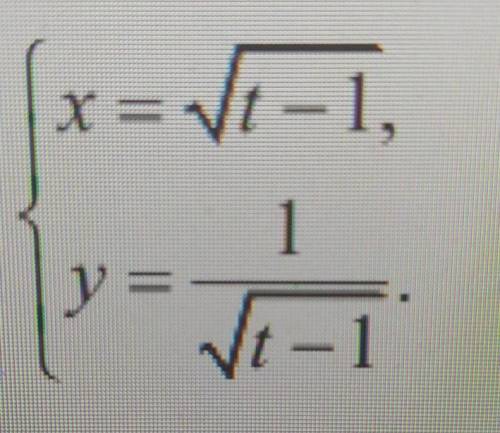
Другие вопросы по теме Алгебра
Популярные вопросы
- Значение пословицы в чужом краю и летом холодно...
1 - Найдите точку пересечения графиков линейных функций у=3х-2 и у=-2х+3...
1 - Фирма «липки» оказывает услуги по благоустройству дворовых территорий....
2 - Дробь 5/38 и 10/29 к наименьшему общему знаменателю...
2 - Принадлежит ли графику у=-3х+1 точки а(-3; 10) и в(4; -13) ....
3 - Раскройте скобки, поставив глагол в нужную форму 1) jim ( live ) near...
1 - Верно ли, 100г составляют 2% от 5 кг...
2 - Расстояние между двумя пунктами катер проплывает по озеру за 3 часа.такое...
1 - Однажды нам задали 2 по . я не смог решить. портной купил отрез ткани...
2 - Входят ли в активное население безработные?...
2
Итак, начнем с первой производной.
1. Применим правило дифференцирования для функции y = (3x^2 - 5x + 2)^3:
Для этого выражения будем использовать правило цепной линейки, поэтому умножим найденную производную на производную внутренней функции.
Внутренняя функция: u = 3x^2 - 5x + 2.
Внешняя функция: y = u^3.
Найдем первую производную внутренней функции:
u' = (3x^2 - 5x + 2)' = 6x - 5.
Теперь найдем первую производную внешней функции, используя правило цепной линейки:
y' = 3(u^2 * u') = 3((3x^2 - 5x + 2)^2 * (6x - 5)).
Упростим это выражение:
y' = 3(9x^4 - 30x^3 + 24x^2 - 20x + 4) * (6x - 5).
Распространим скобки и упростим еще больше:
y' = (54x^5 - 405x^4 + 890x^3 - 860x^2 + 376x - 60).
Теперь перейдем ко второй производной.
2. Будем продолжать использовать правило цепной линейки, чтобы продифференцировать найденную первую производную.
Теперь производная внутренней функции будет u' = 6x - 5.
Найдем вторую производную внешней функции:
y'' = 3((6x - 5)^2 * (6x - 5)) = 3(36x^2 - 60x + 25) * (6x - 5).
Распространим скобки и упростим выражение:
y'' = (108x^3 - 330x^2 + 345x - 125).
Таким образом, мы нашли производную второго порядка для данной функции:
y'' = 108x^3 - 330x^2 + 345x - 125.
Чтобы получить полное решение, необходимо еще указать область определения данной функции, а также ее интервалы возрастания и убывания.