1. Алгебра
  2. Найти производную сложной

Найти производную сложной функции. 1) y = ctg2x
2) y= (2x^3 - 3x)^4
3) y=7^x

ankavasilenko2 ankavasilenko2    3   25.09.2021 11:26    1

Ответы
Groyve1 Groyve1  25.09.2021 11:30

как то так по формулам

Объяснение:

y = ctg2x

y'=(ctg2x)'*(2x)'=-\frac{1}{sin^22x}*2=-\frac{2}{sin^22x}

y= (2x^3 - 3x)^4

y'=((2x^3-3x)^4)'=4(2x^3-3x)^3*(2x^3-3x)'=4(2x^3-3x)^3*(6x^2-3)

y=7^x

y'=(7^x)'=7^xln7

2)(cosu)'=-sinu*u'

формула где u-любое выражение

cos меняется по стандартной формуле

3) (c^x\\)'=c^x\\*lnc*x'

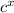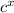
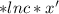
c-любое число

опять таки формула которую нас заставляют учить

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
laxier laxier  15.08.2019 01:30
Найдите число, 20% которого равно 5...
kskkksjsjsj kskkksjsjsj  15.08.2019 01:30
При каких значениях х: 1) выражение 6х^2+5х-20 принимает значение, равное -9 2)значение выражений 13х^2+х+10 и 5х^2+17 равны 3) значение выражений 3х^4+4х^4-23 и -9+х+3х^4...
BaSfOr BaSfOr  15.08.2019 01:30
Найдите значение ,при котором парабола y=2x^-12x+c касается оси x. если что,то ^=2...
polina200412 polina200412  15.08.2019 01:30
Найдите корень уравнения -y+8-14y=23 желательно с разъяснениями, чтобы лучше понять тему...
Валоронтеа Валоронтеа  15.08.2019 01:30
Найдите нули функции: y = i8x² - 1i - ix+1i...
schapalenko schapalenko  15.08.2019 01:30
Вгруппе студентов 17 юношей и 8 девушек.какова вероятность что студент, фамилия которого в списке группы находится на первом месте,окажется девушкой?...
Ksu1ma Ksu1ma  14.05.2020 14:50
В таблице приведены данные о размере премий, выплаченных сотруднику в 2018 и 2019 годах. Какую в среднем премию за квартал получал сотрудник в 2018 году?...
Анна157211цаа Анна157211цаа  14.05.2020 14:50
Найди все те значения x, при которых функция не определена: 16x2−4/x2−4x+4. ответ: при x=...
Сельга7 Сельга7  14.05.2020 14:50
рівняння, первісна функція, площа...
tyranball tyranball  14.05.2020 14:50
Один робітник працював за станком 3 год,а інший-4 год.За цей час вони виготовили 88 деталей.Скільки деталей виготовив кожний робітник,якщо за 1 год роботи вони разом...

Популярные вопросы