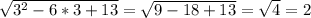Найти производную функции и её наименьшее значение: у=√ х²-6х+13
Другие вопросы по теме Алгебра
Популярные вопросы
- Люди очень нужно тут всё нужно, мне до среды крайний срок ...
3 - 2. Укажите предложение, в котором есть обособленное определение: а) Здесь...
2 - Вычисли, какая масса гидроксида никеля(II) выпадет в осадок при взаимодействии...
2 - найти сумму натуральных чисел от 1 до 100 включительно.Дано: 1, 2, 3,...
1 - Химия. Пальмитиновая кислота НЕ реагирует с: 1)Ca(OH)2 2)C6H12 3)H2 4)C4H9OH...
1 - В треугольнике АВС, угол С - прямой, Угол А = 30 градусов, ВС =6 см. Найдите...
3 - Сочинение на лингвистическую тему по русскому языку...
1 - Найти корни уровнения d^2-16d-17=0...
3 - Условие задания:Запиши произведение(x+y)(x+y)-(x+y):(x+y)n разв виде степени.(Вводи...
1 - 1. Отметь предложение, в котором есть обособленный член предложения, (знаки...
3
D(y):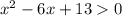
y'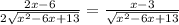
y'=0 при x-3=0 x=3
К критическим точкам относятся те, в которых прозводная равна 0 или не существует
D(y'):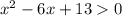
Но те значения, которые x не может принимать не входят в D(y)=> cуществует только одна критическая точка, которая является точкой минимума
y(3)=