Найти производную функции:
f(x)=2x+5/x+3
Другие вопросы по теме Алгебра
Популярные вопросы
- Составить текст из 4-5 предложений в которых будут содержатся вводные...
3 - Проезжая по улице,барин увидел,что сыновья данилы обуты в сапожки.и...
3 - При трении эбонитовой палочки о шерсть электроны 1 вещества переходят...
1 - Со станций одновременно в противоположном направлениях отправились...
1 - Придумайте, , две сказки 1-я сказка с 10 парами омонимов, а 2-я...
3 - Решите преобразуйте выражение в многочлен 1.(5а+1\5b)^2 2.(1\4m-2n)^2...
1 - Уани было 125 тенге, а у каната 194 тенге после того как аня купила...
1 - Тюльпан - он простой или сложный? черешковый или сидячий? тип жилкование?...
2 - Человек в год в среднем должен выпивать 150 литров молока, что...
3 - Укажите,какие природные явления относятся к стихийным бедствиям.варианты:...
1
f'(x)=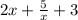
f'(x)=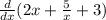
используем правило дифференцирования:
f'(x)=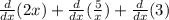
вычисляем производное:
f'(x)=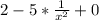
упрощаем выражение:
f'(x)=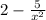 это и есть наш ответ
это и есть наш ответ