Найти произведения корней квадратного трехчлена x³=-1 help
Другие вопросы по теме Алгебра
Популярные вопросы
- Как возникали государства в древности?...
1 - Просклонять простое предложение по временам языка предложение i...
3 - Загрязнение окружающей среды отрицательно влияет на здоровье человека.разбор...
2 - 2so2+4naoh=2na2so3+2h2o. уравнения правилно...
3 - 1)отметьте на координатнойм луче с единичным отрезков равным 1...
3 - Из 200 автомобилей каждые 120 имеют неисправность световой системы,...
1 - Два автомобиля едут навстречу друг другу.сейчас между ними 60 километров.скорость...
1 - Вчем состоит художественное своеобразие повести временных лет...
2 - Объясните : постройте графики зависимости проекций векторов скорости...
2 - Какие ископаемые формы людей принято относить к древнейшим? 1)...
2
У вас не квадратный трёхчлен.
В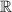 (вещественных числах):
(вещественных числах):
В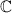 (комплексных числах):
(комплексных числах):
Перемножив корни также получим -1