Найти произведение корней уравнения один большой корень из 23-х=х-3 √23-х=х-3

ответ: x = 7.

Объяснение:

ОДЗ: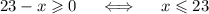

Возводим обе части уравнения до квадрата, при условии, что правая часть принимает неотрицательные значения: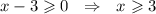

По теореме Виета

x₁ = 7

x₂ = -2 - не удовлетворяет условию

Проверка: x=7: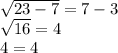  

ОДЗ: 23-x≥0, х≤23

x-3≥0, х≥3

Возводим обе части уравнения в квадрат, при этом могут появиться посторонние корни, нужно проверить корни.

23-x=х²-6x+9

х²-5х-14=0

По теореме, обратной теореме Виета

x₁ = 7

x₂ = -2 - не удовлетворяет условию

Проверка: x=7:  √(23-7)=7-3

4=4

ответ х=7