Найти при каких значениях производная функции меньше нуля

Другие вопросы по теме Алгебра
Популярные вопросы
- Решите уравнение 1/4х+5=21-1/12...
3 - написать краткое изложение по английскому: Тринити Колледж в Дублине: 400 лет истории...
3 - Підготуйте повідомлення про деякі легенди (на вибір): 1) заснування рима. 2)викрадення...
1 - №4 «Уберите лишнее» Задание: Что не является частью нефрона?1.Извитой каналец 5....
3 - с тремя во Как и почему сочетаются в схеме финансовой системы элементы по разным...
1 - Укажите с графика, чему равно значение y при x=1,5...
2 - 1)Маляр за минуту красит 2 м 2 стены. Задайте зависимость площади закрашенной стены...
2 - РЕШИТЕ Употребление приставок il-, ir-, im-, in-, un-, dis-, mis-, non- Образуйте...
2 - В чём разница между музыкальными портретами реального человека из сказочных героев??...
3 - А1. Найдите неправильное утверждение. 1) союз — это служебная часть речи 2) союзы...
3
Объяснение:
Для начала найдем производную данной функции
1. Используем формулу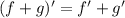
2. Используем формулу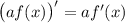
3. Найдем производную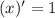
4. Используем формулу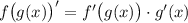 , где
, где
Решим неравенство
см. на рисунок