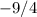НАЙТИ ПРЕДЕЛ ФУНКЦИИ. ПОДРОБНО!
Другие вопросы по теме Алгебра
Популярные вопросы
- Порівняйте 40% числа 80 і 80% числа 40 напишыте с решением...
1 - Сумою чисел 537 + 492 + 463 + 408 є числоа1800б1700в2000г1900...
1 - Уж как пал туман на сине море где здесь частицы...
2 - Запишите предложение, заменяя прямую речь косвенной. Правильно расставьте...
3 - літо у вірші Максима Рильського справляєліто у вірші Максима Рильського...
3 - решить уравнение: 1 7/8x = -1 - (- 3/4) 2^...
2 - Вопросы по произведению А. Сент-Экзюпери « Маленький принц» 1)Расскажите...
1 - Распределите особенности по соответствующим категориям мусульманское...
3 - Стеклянный аквариум имеет ширину 40 см, что составляет4/5 - от его...
2 - Правило how...? questione с объяснениямиp.s тот, кто объяснит получит...
3
Предварительно вспомним некоторые результаты:
Выражение под пределом можно переписать: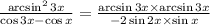 ; Теперь домножим на
; Теперь домножим на 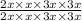 - это единица, поэтому ничего не изменится. Получим:
- это единица, поэтому ничего не изменится. Получим: 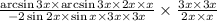 ; При
; При  можно воспользоваться обозначенными выше результатами. Тогда получим
можно воспользоваться обозначенными выше результатами. Тогда получим 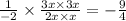 ;
;
ответ: