Найти площадь заштрихованной фигуры, где f(x)=a√x + b, g(x)=kx

Question

Алгебра: Найти площадь заштрихованной фигуры, где f(x)=a√x + b, g(x)=kx

linvliv · Answer

1) Т.к. график f(x) проходит через (0; 3), то b=3.

Т.к. график f(x) проходит через (9; 9), то 3а+3=9 ⇒ а=2.

Тогда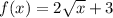 $f(x)=2\sqrt{x}+3$

Т.к. график g(x) проходит через (0; 0), и (9; 9), и является частью прямой, то k=1. Тогда g(x) = х.

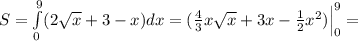
2) $S=\int\limits_{0}^{9}(2\sqrt{x}+3-x)}dx=(\frac{4}{3}x\sqrt{x}+3x-\frac{1}{2}x^2)\Big|_0^9=$

$=\frac{4}{3}\cdot9\sqrt{9}+3\cdot9-\frac{1}{2}\cdot9^2=36+27-40,5=22,5$

ответ: 22,5