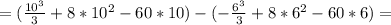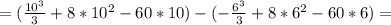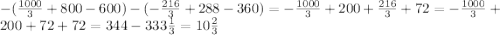Найти площадь ограниченную параболой и осью ox y= -x^2+16*x-60
Другие вопросы по теме Алгебра
Популярные вопросы
- Язык 9 класс (сразу все, с одним не отвечайте)...
2 - Запиши выражение и найди их значение ...
3 - Найти [tex]\frac{dy}{dx}[/tex] и [tex]\frac{d^{2}y }{dx^{2} }[/tex]...
3 - А1. какие основные события происходят во втором действии? кратко пере-скажите,...
1 - 1.как вы считаете, какие сходства и различия имеются между погодой...
2 - Решить уравнение: - (4,1x + 2,5) - (2,3x + 3,9) = 1,6x решить уравнение:...
1 - Решите неравенство и изображений множество его решений на координатной...
1 - Площадь меньшего поршня гидравлического пресса 15 см², площадь поршня...
1 - Найдите слова соответствуют хаьар , ғылыми болжам . гибель великой...
1 - Дайте ответы. это для контрольной поэтому напишите ответ нормальным...
1
∫ -x^2+16*x-60=-x^3/3+8x^2-60x
x1=6
x2=10
S=-1000/3+800-600+6^3/3-8*36+360=560+72-8*36-1000/3=344-1000/3=10 2/3
Парабола пересекает ось OX в точках 6 и 10. Это будут пределы интегрирования
6 - нижний, 10 - верхний
S =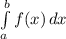
Найдём первообразную функции чтоб не переписывать в решение
F(x) = F(-x^2+16*x-60) =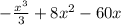
Во вставках уравнения не хочет писать предел 10, так что обозначу 10 как b
Теперь
S =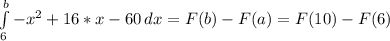 =
=