Найти площадь криволинейной трапеции ограниченной графиком функции , осью ox и прямыми x=1 и x=4
Ответы
Определенный интеграл 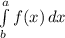 численно равен площади криволинейной трапеции, ограниченной сверху графиком функции
численно равен площади криволинейной трапеции, ограниченной сверху графиком функции 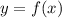 , снизу прямой
, снизу прямой 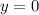 , слева и справа прямыми
, слева и справа прямыми  и
и 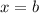 .
.
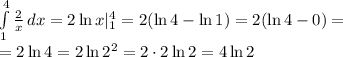
ПОКАЗАТЬ ОТВЕТЫ
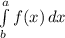 численно равен площади криволинейной трапеции, ограниченной сверху графиком функции
численно равен площади криволинейной трапеции, ограниченной сверху графиком функции 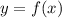 , снизу прямой
, снизу прямой 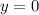 , слева и справа прямыми
, слева и справа прямыми  и
и 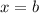 .
.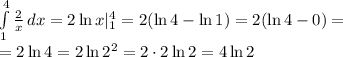
Другие вопросы по теме Алгебра
Популярные вопросы
- Зайырлы мемлекет созине кластер...
2 - Выберите жанры симейного фольклора и цифры запишите в бланк ответов...
2 - Вариант 2. №1. Переведите масштаб: 1: 600 000 1: 35 000 1: 700 1: 9000 в...
1 - Самолёт отрывается от земли при скорости 72 км/ч. Какую мощность развивает...
1 - Постройте график функции: y= -2(x+1)²-3...
3 - Зерттеуді ұсыну формалары ...
1 - 2. Герой вспоминает свою учительницу французского языка как очень доброго,...
3 - Желательно с дано за ранее!...
3 - 1. Первоначальный район расселения тюркских племен: А) Семиречье Б) Алтай...
3 - 60 0 2 - 100 зависимости вдоль а х(t) для оси Х. Какой И 2. На рисунке изображены...
1