Найти площадь криволинейной трапеции ограниченной графиком функции , осью ox и прямыми x=0 и x=2
Ответы
Определенный интеграл 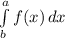 численно раен площади криволинейной трапеции, ограниченной сверху графиком функции
численно раен площади криволинейной трапеции, ограниченной сверху графиком функции 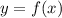 , снизу прямой
, снизу прямой 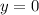 , слева и справа прямыми
, слева и справа прямыми  и
и 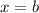 .
.
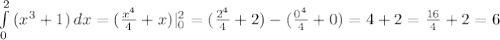
ПОКАЗАТЬ ОТВЕТЫ
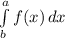 численно раен площади криволинейной трапеции, ограниченной сверху графиком функции
численно раен площади криволинейной трапеции, ограниченной сверху графиком функции 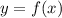 , снизу прямой
, снизу прямой 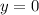 , слева и справа прямыми
, слева и справа прямыми  и
и 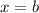 .
.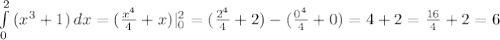
Лучше конечно начертить график функции, но пишу с планшета, потому буду решать аналитически. Границы трапеции определены условием задания это 0 и 2, то есть искомая трапеция находится в этих пределах. Геометрический смысл интеграла это площадь, потому решаем интеграл: 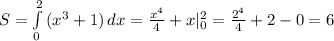 . ответ: 6 ед².
. ответ: 6 ед².
ПОКАЗАТЬ ОТВЕТЫ
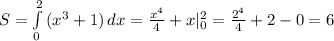 . ответ: 6 ед².
. ответ: 6 ед².
Другие вопросы по теме Алгебра
Популярные вопросы
- Дан одномерный массив целых чисел состоящий из 22 двух элементов посчитать количество...
1 - Подскажите как решить . у зайчика было 19морковок.он сьел5м.утром,а в обед еще...
2 - Число 16 меньше задуманного числа в 4 раза уровнение...
2 - Найти область определения функций y=-дробь -7х-5 (-х-1)х...
3 - (x-2)y=6 x-2y=6 решите графически систему уравнений...
1 - Вкаких случаях ставятся do does don`t doesn`t? завтра к/р, та тема плохо запомнилась...
3 - Длина отрезка равна 3 дм 5 см.какова длина его пятой части...
2 - Заменить * так,чтобы равенство 32/8=*/17 сохранилось. а)72 б)76 в)64 г)42 д)68...
2 - Всосуде было 5 куб.см воды. отметь уровень воды в этом сосуде после того как...
3 - Фонетичний розбір слова бiлiють обсипанi...
2